TOÁN 8 | HUYNHMANHHUNGWeb

Tính các đại lượng hình học bằng cách lập phương trình

Posted on September 10, 2008 by goldhung

Để tính toán các đại lượng hình học chúng ta có nhiều cách tính: tính trực tiếp, vẽ đường phụ,…và hôm nay chúng ta cùng tìm hiểu một cách nữa đó là : lập phương trình để tính toán các đại lượng hình học. Chúng ta xét các ví dụ sau:

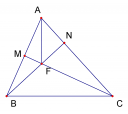
Ví dụ 1: Cho tam giác ABC vuông tại A, đường phân giác trong $BD = a\sqrt{3}, DC= 3DA$ . Tính các cạnh của tam giác ABC.

Hướng dẫn giài:

Đặt $AD = x$ . Vì BD là phân giác trong góc B nên ta có:

$\dfrac{1}{3} = \dfrac{AD}{DC} = \dfrac{AB}{BC} \Rightarrow CB =3 AB = 3x$

Áp dụng định lý Pytagore cho các tam giác vuông ABC và ADB ta có:

+ $AC^2 = BC^2 - AB^2 = 9AB^2 - AB^2= 8AB^2$ hay $(4x)^2 = 8AB^2 \Leftrightarrow AB^2 = 2x^2$

+ $AB^2 = BD^2 - AD^2 = (a\sqrt{3})^2 - x^2 = 3a^2 - x^2$

Do đó ta có phương trình $2x^2 = 3a^2 - x^2 \Leftrightarrow x = a$

Vậy $AC = 4x = 4a, AB = \sqrt{2} a, BC = 3AB = 3\sqrt{2}a$

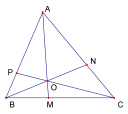
Ví dụ 2: Cho tam giác ABC vuông có $AB = c, AC = b$ . M là một điểm trên cạnh BC. Biết tỉ số khoàng cách từ M đền AB và AC bằng $k$ . Tính AM.

Hướng dẫn giài:

Vẽ $latex MH \bot AC, MK \bot AB (H \in AC, K \in AB). Khi đó ta có:

$\dfrac{MK}{MH} = k$

Đặt $MH = x \Rightarrow MK = kx$ .

Ta có MK // AC nên $\dfrac{MK}{AC} = \dfrac{BM}{AC}$

và MH // AB nên $\dfrac{MH}{AB} = \dfrac{MC}{BC}$

Do đó $\dfrac{MK}{AC} +\dfrac{MH}{AB} =\dfrac{BM}{AC} +\dfrac{MC}{BC} = 1$

hay $\dfrac{kx}{b} +\dfrac{x}{c} = 1$

Giải ra ta được $x =\dfrac{bc}{b+ck}$

Từ đó ta có :

$AM^2 = AH^2 + MH^2 = MI^2 + MH^2 = x^2 + k^2x^2 =$

$x^2(1+k^2) = \left(\dfrac{bc}{c+bk}\right)^2(1+k^2)$

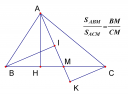
Ví dụ 3: Cho tam giác ABC vuôn tại A, đường cao AH, M là trung điểm của BC. Cho AB = 2a, MH = a. Tính các cạnh của tam giác ABC.

Hướng dẫn giài:

Đặt $BC = 2x \Rightarrow AM = BM = CM = x$ . Ta có $BC > AB \Rightarrow x > a$

Ta chứng minh được:

$\triangle CHA \sim \triangle CAB (gg) \Rightarrow \dfrac{CH}{CA} = \dfrac{CA}{CB}$

$\Rightarrow CA^2 = CB.CH (1)$

Mặt khác áp dụng định lý Pytagore cho tam giác ABC ta có: $BC^2 = AB^2 + AC^2 \Rightarrow AC^2 = BC^2 - AB^2 = 4x^2 - 4a^2 (2)$

Xét hai trường hợp:

+ H nằm giữa B và M, khi đó $CH = CM + HM = x + a$

Từ (1) và (2) ta có phương trình:

$2x(x+a) = 4x^2 - 4a^2 \Leftrightarrow x^2 - ax - 2a^2 = 0$

$\Leftrightarrow (x+a)(x-2a) = 0 \Leftrightarrow x = 2a$

+ H nằm gữa C và M, khi đó ta có $CH = CM - HM = x - a$

Từ (1) và (2) ta có phương trình:

$2x(x-a) = 4x^2 - 4a^2 \Leftrightarrow x^2 +ax - 2a^2 = 0$

$\Leftrightarrow (x-a)(x+2a) = 0 \Leftrightarrow x = a$

( không thỏa)

Vậy $BC = 2x = 4a, AC = 2\sqrt{3}a$

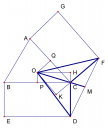
Ví dụ 4: Cho hình thang cân ABCD có đáy nhỏ AB = 2a, chiều cao bằng $\sqrt{3}a$ , đường chéo BD vuông góc với cạnh bên BC. Tính đáy lớn và cạnh bên.

Hướng dẫn giài:

Gọi H và K là hình chiếu của AB trên CD. Ta có $DH = CK, AB = HK = 2a, BK = a$

Đặt $CK = x$ . Ta có $\triangle CKB \sim BKD (g.g) \Rightarrow \dfrac{CK}{BK} =\dfrac{BK}{KD} \Rightarrow BK^2 = CK.KD$ .

hay $3a^2 = x(2a+ x)$

Giải phương trình ta được $x = a$

Vậy $CD = 4a, BC = \sqrt{2}a$

Bài tập rèn luyện thêm:

Bái 1:

Cho tam giác ABC vuông tại A, đường cao $AH = \dfrac{\sqrt{6}}{3}$ , đường trung tuyến $CM = \dfrac{3}{2}AB$ . Tính các cạnh của tam giác.

Bài 2:

Cho tam giác ABC vuông tại A có đường phân giác trong vuông góc với đường trung tuyến BM. Tính các cạnh của tam giác ABC biết $AD =\sqrt{2} l$ .

Bài 3:

Tính diện tích tam giác ABC có đường cao AH = 6cm, biết rằng AH chia góc A theo tỉ số 1 : 2 và chia cạnh BC thành hai phần mà đoạn nhỏ bằng 3cm.

Bài 4:

Điểm M nằm trên cạnh huyền của một tam giác vuông diện tích $100cm^2$ và có khoảng cách đến hai cạnh góc vuông bằng 4cm và 8cm. Tính độ dài hai cạnh góc vuông.

Bài 5:

Tính diện tích của tam giác ABC biết độ dài 3 cạnh lần lượt là 4cm, 6cm và 8cm.

Bài 6:

Chứng minh rằng diện tích tam giác có độ dài các cạnh a, b, c là : $\sqrt{p(p-a)(p-b)(p-c)}$ . Trong đó p là nửa chu vi của tam giác. (Công thức Hê-rông)

Filed under: TOÁN 8 | Leave a comment »

Bài Toán Tỉ Số Diện Tích Và ứng Dụng (phần 2)

Posted on August 30, 2008 by goldhung

Bài 1: Cho tam giác ABC. M là trung điểm của AB, N là điểm thuộc cạnh AC sao cho AC = AN. Gọi K là giao điểm của BN và CM. Chứng minh KC = 4KM.

Hướng dẫn giải:

Ta có $\dfrac{S_{ABK}}{S_{CBK}} = \dfrac{AN}{CN} =\dfrac{1}{2}$ và $\dfrac{S_{KBM}}{S_{KBA}} =\dfrac{BN}{AB} =\dfrac{1}{2}$

Suy ra $\dfrac{S_{KBM}}{S_{CBK}} =\dfrac{1}{4}$ , suy ra $\dfrac{MK}{CK}=\dfrac{S_{KBM}}{S_{CBK}} =\dfrac{1}{4} \Rightarrow CK = 4MK$

Bài 2: Cho tam giác ABC và điểm O nằm trong tam giác. AO, BO, CO lần lượt cắt BC, AC và AB tại M, N, P. Chứng minh: $\dfrac{AO}{AM} +\dfrac{BO}{BN} +\dfrac{CO}{CP} =2$

Hướng dẫn giải:

Ta có: $\dfrac{AO}{AM} =\dfrac{S_{ABO}}{S_{ABM}} =\dfrac{S_{ACO}}{S_{ACM}} =\dfrac{S_{ABO} +S_{ACO}}{S_ {ABM}+S_{ACM}} = \dfrac{S_{ABO} +S_{ACO}}{S_{ABC}}$

Chứng minh tương tự ta có: $\dfrac{BO}{BN} =\dfrac{S_{ABO} +S_{CBO}}{S_{ABC}}$ và $\dfrac{CO}{CP} =\dfrac{S_{AOC}+S_{BOC}}{S_{ABC}}$

Từ đó suy ra:

$\dfrac{AO}{AM} +\dfrac{BO}{BN} +\dfrac{CO}{CP}$ $=\dfrac{S_{ABO} +S_{ACO}}{S_{ABC}}$ $+ \dfrac{S_{ABO} +S_{CBO}}{S_{ABC}}$ $+\dfrac{S_{AOC}+S_{BOC}}{S_{ABC}} =2$

Bài 3: Cho tam giác ABC, về phía ngoài tam giác dựng hai hình chữ nhật ABDE và ACFG có diện tích bằng nhau. Gọi O là giao điểm các đường trung trực của tam giác ABC. Chứng minh OC đi qua trung điểm của DF.

Hướng dẫn giải:

Ta cần chứng hai tam giác OCD và OCF có diện tích bằng nhau. Vẽ Vẽ OH, OK lần lượt vuông góc với CD và CF(H thuộc CD, K thuộc CF). Ta chứng minh được $OH = \dfrac{1}{2}BC, OK=\dfrac{1}{2}AC$ . Từ đó suy ra:
$S_{OCD} = \dfrac{1}{2}OH.CD =\dfrac{1}{4}BC.CD =\dfrac{1}{4}S_{BCDE}$ và $S_{OCF} =\dfrac{1}{4}S_{ACFG}$
Mà $S_{BCDE} = S_{ACFG}$ nên ta có: $S_{OCD} =S_{OCF}$ . Từ đó ta có: OC đi qua trung điểm của DF

Filed under: TOÁN 8 | Leave a comment »

Bài Toán Về Tỉ Số Diện Tích Và Ứng Dụng(Phân1)

Posted on August 30, 2008 by goldhung

Bài toán 1: Cho tam giác ABC, M là một điểm thuộc đường thẳng BC.

a) Chứng minh: $\dfrac{S_{ABM}}{S_{ACM}} = \dfrac{BM}{CM}$ .

b) Gọi I và K là hình chiếu của B và C trên AM. Chứng minh: $\dfrac{S_{ABM}}{S_{ACM}} = \dfrac{BI}{CK}$ .

Giải:

a) Vẽ $AH \bot BC (H in BC)$ . Khi đó ta có:

$\dfrac{S_{ABM}}{S_{ACM}}= \dfrac{\dfrac{1}{2} AH. BM}{\dfrac{1}{2}AH.CM} = \dfrac{BM}{CM}$

b) Ta có $\dfrac{S_{ABM}}{S_{ACM}}= \dfrac{\dfrac{1}{2} AM. BI}{\dfrac{1}{2}AM.CK} = \dfrac{BI}{CK}$

Hệ quả 1: Cho tam giác ABC, M thuộc đường thẳng BC thì $S_{ABM} = S_{ACM} \Leftrightarrow M$ là trung điểm BC.

Hệ quả 2: Cho tam giác ABC, và một điểm M bất kì. Khi đó nếu $S_{ABM} =S_{ACM}$ thì $AM // BC$ hoặc AM đi qua trung điểm của BC.

Hệ quả 3: Cho tam giác ABC, G là một điểm bất kì. Khi đó G là trọng tâm của tam giác ABC khi và chỉ khi $S_{GAB} =S_{GBC} =S_{GAC}$ .

Bài toán 2: Cho tam giác ABC. D và E là hai điểm thuộc cạnh AB và AC. Khi đó $\dfrac{S_{ADE}}{S_{ABC}} =\dfrac{AD.AE}{AB.AC}$

Giải:

Theo bài toán 1 ta có: $\dfrac{S_{ADE}}{S_{ABE}}= \dfrac{AD}{AB}$ và $\dfrac{S_{ABE}}{S_{ABC}}= \dfrac{AE}{AC}$

Suy ra: $\dfrac{S_{ADE}}{S_{ABC}} = \dfrac{S_{ADE}}{S_{ABE}}.\dfrac{S_{ABE}}{S_{ABC}} = \dfrac{AD.AE}{AB.AC}$ .

Chú ý: Kết quả của bài toán vẫn còn đúng nếu D, E thuộc đường thẳng AB và AC.

Hệ quả 1: Nếu hai tam giác ABC và MNP có $\widehat{A} = \widehat{M}$ hoặc $\widehat{A} +\widehat{M} =180^o$ thì $\dfrac{S_{ABC}}{S_{MNP}} =\dfrac{AB.AC}{MN.MP}$

Hệ quả 2: Tỉ số hai tam giác đồng dạng bằng bình phương tỉ số đồng dạng. Nghĩa là: nếu tam giác ABC và tam giác MNP đồng dạng thì: $\dfrac{S_{ABC}}{S_{MNP}} = \dfrac{AB^2}{MN^2}$