TOÁN 9 | HUYNHMANHHUNGWeb

phương pháp Chứng minh tứ giác nội tiếp

Posted on August 23, 2008 by goldhung

Để chứng minh một tứ giác là tứ giác nội tiếp ta có các cách sau:

Cách 1: Chứng minh tổng hai góc đối bằng $180^o$ .

Cách 2: Chứng minh góc ngoài bằng góc trong đỉnh đối.

Cách 3: Chứng minh hai đỉnh kể cùng nhìn một cạnh hai góc bằng nhau.

Cách 4: Chứng minh 4 đỉnh cách đều một điểm.

Các cách trên chủ yếu là các cách chứng minh dựa vào các chứng minh về góc. Ngoài các cách trên chúng ta có một vài điều kiện đủ khác để một tứ giác là tứ giác nội tiếp. Chúng ta xét bài toán sau:

Bài 1: Cho tứ giác ABCD, gọi O là giao điểm hai đường chéo và I là giao điểm hai cạnh bên AD và BC. Chứng minh rằng:

a) Tứ giác ABCD nội tiếp khi và chỉ khi OA.OC = OB.OD

b) Tứ giác ABCD nội tiếp khi và chỉ khi IA. ID = IB. IC

Việc chứng minh bài toán này không có gì khó khăn, chúng ta chỉ việc chứng minh các tam đồng dạng và suy ra kết quả. Nhưng qua bài toán trên cho ta một ý tưởng chứng minh tứ giác nội tiếp đó là chứng minh một đẳng thức về cạnh.

Hãy dùng ý tưởng đó để giải các bài toán sau:

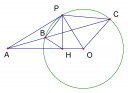
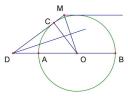
Bài 2: Cho đườn tròn (O), A là một điểm nằm ngoài đường tròn. Một cát tuyến qua A cắt (O) tại B và C. Vẽ tiếp tuyến QP với (O) (P là tiếp điểm), gọi H là hình chiếu của P trên OA. Chứng minh 4 điểm O, H, B, C cùng thuộc một đường tròn.

Hướng dẫn giải:

Chúng ta thấy BC và OH cắt nhau tại A, do đó để chứng minh tứ giác OHBC nội tiếp ta nghĩ đến việc chứng minh AH.AO = AB.AC.

Thật vậy ta có:

$AH.AO = AP^2$ (hệ thức lượng trong tam giác vuông APO)

$AB.AC = AP^2$ (tam giác APB và ACP đồng dạng).

Từ đó ta có $AH.AO = AB.AC$ , theo bài 1 ta có điều cần chứng minh.

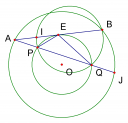
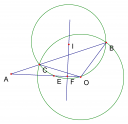
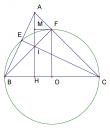
Bài 3: Cho tam giác cân ABC (AB = AC). Đường tròn tâm O tiếp xúc với AB tại B và tiếp xúc với AC tại C. Gọi H là giao điểm của OA và BC. Vẽ dây cung DE của (O) đi qua H. Chứng minh rằng tứ giác ADOE nội tiếp.

Hướng dẫn giải

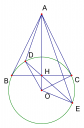
Tam giác OCA vuông tại C, CH là đường cao nên ta có: $HO.HA = HC^2$

Dây cung BC và DE của (O) cắt nhau tại H nên ta có $HD.HE = HB.HC = HC^2$

Từ đó ta có $HA.HO = HD.HE$ , chứng minh tương tự bài 1 ta có tứ giác ADOE nội tiếp.

Bài tập

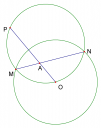
Bài 1: Cho đườn tròn (O; R) và một điểm I nằm trong đường tròn. Hai dây cung AB và CD cùng đi qua I. Tiếp tuyến tại A và B cắt nhau tại P, tiếp tuyến tại C và D cắt nhau tại Q. Gọi M là giao điểm của OQ và CD, N là giao điểm của OQ và AB. Chứng minh:

a) Tứ giác MNPQ nội tiếp.

b) OI vuông góc với PQ.

Bài 2: Cho hình thang vuông ABCD ( AB//CD). Gọi O là trung điểm của AD. Đường thẳng qua A vuông góc với OB cắt đường thẳng qua D vuông góc với OC tại K. Chứng minh OK vuông góc với BC.

Filed under: TOÁN 9 | Leave a comment »

Một số bài toán SGK đến bài toán HSG

Posted on August 23, 2008 by goldhung

Bài toán 1:

Cho đường tròn (O; R) và một điểm M cố định không nằm trên đường tròn. Qua M kẻ hai đường thẳng. Đường thẳng thứ nhất cắt (O) tại A và B, đường thẳng thứ hai cắt (O) tại C và D. Chứng minh MA.MB = MC.MD

Chứng minh bài toán này không khó bằng cách xét hai trường hợp M nằm ngoài và nằm trong đường tròn (O). Trong mỗi trường hợp chứng minh tam giác MAC và tamg giác MCD đồng dạng, từ đó ta suy ra kết quả cần chứng minh.

Qua bài toán này ta có thể chứng minh bài toán sau:

Bài toán 2:

Nếu M không nằm trên đường tròn (O; R), một đường thẳng thay đổi qua M và cắt (O) tại A và B. Khi đó tích MA. MB không đổi và bằng $|OM^2 - R^2|$

Chứng minh bài toán 2 chỉ cần vẽ đường thẳng qua M và O cắt (O) tại C, D. Sau đó chứng minh tương tự bài toán 1 ta được kết quả.

Bài toán 2 cho ta một ý tưởng để giải các bài toán về họ đường tròn đi qua một điểm cố định. Ta cùng xét các bài toán sau:

Bài toán 3 ( Năng Khiếu 2004 – 2005 Chuyên toán) Cho đường tròn (O) và một điểm A khác O nằm trong đường tròn. Một đường thẳng thay đổi qua A nhưng không đi qua O cắt (O) tại M và N. Chứng minh rằng đường tròn ngoại tiếp tam giác OMN luôn đi qua một điểm cố định khác O.

Gọi P là giao điểm của đường tròn ngoại tiếp tam giác OMN và tia đối của tia AO. Ta có $AP.AO = AM.AN \Rightarrow AP = \dfrac{AM.AN}{AO}$ không đổi vì A và (O) cố định. Hơn nữa P thuộc tia đối của tia AO cố định nên P là điểm cố định.

Bài toán 4: (NK 2006 – 2007 Chuyên toán) Cho đường tròn (O), AB là một dây cung cố định và E là trung điểm của AB. Một đường thẳng thay đổi qua A cắt đường tròn tâm O bán kính OE tại P và Q. Chứng minh rằng tích AP. AQ không đổi và đường tròn ngoại tiếp tam giác BPQ luôn đi qua một điểm cố định.

Vì E là trung điểm của AB nên OE vuông góc với AB, suy ra AB là tiếp tuyến của (O; OE). Ta chứng minh được $AP.AQ = AE^2=\dfrac{AB^2}{4}$ không đổi.

Gọi I là giao điểm của đường tròn ngoại tiếp tam giác BPQ và AB. Khi đó ta có: $AI.AB = AP.AQ \Rightarrow AI = \dfrac{AP.AQ}{AB}$ không đổi. Suy ra I là điểm cố định.

Bài toán 5: (HSG Q. Tân Bình 2005 – 2006) Từ điểm A nằm ngoài đường tròn (O) vẽ các tuyến ABC (B, C thuộc (O)). Chứng minh rằng khi cát tuyến thay đổi thì tâm đường tròn ngoại tiếp tam giác OBC luôn thuộc một đường thẳng cố định.

Gọi E là giao điểm của đường tròn ngoại tiếp tam giác OBC và AO. Tương tự như hai bài trên ta chứng minh được E là điểm cố định. Từ đó suy ra tâm đường tròn ngoại tiếp tam giác OBC luôn thuộc đường trung trực của OE.

Bài tập

Bài 1: Cho đường tròn (O) và đường thẳng d không cắt (O). M là một điểm thay đổi trên d, từ M vẽ hai tiếp tuyến MA và MB đến (O) (A, B là hai tiếp điểm). Chứng minh AB luôn đi qua một điểm cố định.

Bài 2:

Cho đường tròn (O) và một điểm S cố định nằm ngoài đường tròn. AB là đường kính thay đổi. SA, SB cắt (O) tại C và D.

a) Chứng minh đường tròn ngoại tiếp tam giác SAB luôn đi qua một điểm cố định.

b) Chứng minh CD luôn đi qua một điểm cố định.

Bài 3: Cho 3 điểm C, A, B thẳng hàng và được xếp theo thứ tự đó. Một đường tròn (O) thay đổi luôn đi qua A và B. CP, CQ là các tiếp tuyến của (O) (P, Q là tiếp điểm). Chứng minh rằng:

a) P, Q luôn thuộc một đường tròn cố định.

b) Trung điểm M của PQ luôn thuộc một đường tròn cố định.

Filed under: TOÁN 9 | Leave a comment »

Các phương pháp chứng minh tiếp tuyến

Posted on August 23, 2008 by goldhung

Để chứng minh đường thẳng d là tiếp tuyến của đường tròn $(O; R)$ ta dùng các cách sau đây:

Cách 1 : Chứng minh khoảng cách từ O đến d bằng R. Hay nói cách khác ta vẽ $OH \bot d$ , chứng minh $OH = R$ .

Cách 2: Nếu biết d và (O) có một giao điểm là A, ta chỉ cần chứng minh $OA \bot d$ .

Trên đây là hai cách chủ yếu, ngoài ra còn có các cách sau.

Cách 3: Cách này dựa trên bài toán phụ sau:

Cho tam giác ABC nội tiếp đường tròn (O). Tia Ax thỏa $\widehat{xAB} = \widehat{ACB}$ (Ax cùng phía với tia AC đối với đường thẳng AB). Khi đó Ax là tia tiếp tuyến của (O).

Cách này thường dùng để chứng minh một đường thẳng là tiếp tuyến của đường tròn ngoại tiếp tam giác.

Cách 3 trên là một ví dụ cho phương pháp chứng minh trùng khít – một phương pháp rất hiệu quả để chứng minh các bài toán đảo. Và phương pháp này cũng được dùng nhiều trong các bài toán chứng minh tiếp tuyến.

Ví dụ 1:

Cho đường tròn (O) đường kính AB. C là một điểm thay đổi trên đường tròn (O) . Tiếp tuyến của (O) tại C cắt AB tại D.Qua O vẽ đường thẳng vuông góc với phân giác góc ODC, đường này cắt CD tại M. Chứng minh rằng đường thẳng d qua M song song với AB luôn tiếp xúc với (O) khi C thay đổi.

Giải:

Ta thấy rằng đường thẳng d và (O) chưa có giao điểm nào, do đó ta dùng cách 1 để giải bài toán này.

Vẽ $OH \bot d ( H \in d)$ . Ta cần chứng minh OH = OC.

Ta có tam giác DMO cân tại D, suy ra $\widehat{DMO} = \widehat{DOM}$ . Mà $\widehat{HMO} = \widehat{DOM}$ (So le trong).

Nên ta có $\widehat{DMO} = \widehat{HMO}$ .

Từ đó ta có $\triangle CMO = \triangle HMO$ , suy ra OH = OC. Vậy d là tiếp tuyến của (O).

Ví dụ 2 :

Cho tam giác ABC nhọn. Vẽ đường tròn tâm O đường kính BC cắt AB, AC lần lượt tại E và F. BF và CE cắt nhau tại I. Gọi M là trung điểm AI. Chứng minh: MF là tiếp tuyến của (O).

Giải: Ta thấy F là giao điểm của MF và (O). Ta sẽ sử dụng cách 2 để chứng minh. Tức là ta cần chứng minh $\widehat{OFM} =90^o$ .

Ta chứng minh được I là trực tâm của tam giác ABC.

Trong tam giác vuông AFI có FM là trung tuyến nên MF = FA = BI, suy ra tam giác MFA cân tại M, suy ra $\widehat{AFM} = \widehat{FAM}$ .

Ta cũng có:

$\widehat{OFC} = \widehat{OCF}$

(Tam giác OCF cân tại O).

Từ đó: $\widehat{AFM}+\widehat{OFC}= \widehat{MAF}+ \widehat{OCF}= 90^o$ . Suy ra $\widehat{MFA}=90^o$ . Vậy $OF \bot FM, F \in (O)$ nên MF là tiếp tuyến của (O).